
Credit: Allison Filice for Quanta Magazine.
Imagine a garden filled with every variety of flower in the world — delicate orchids, towering sunflowers, the waxy blossoms of the saguaro cactus and the corpse flower’s putrid eruptions. Now imagine that all that floral diversity reduced to just two varieties, and that by crossbreeding those two you could produce all the rest.
That is the nature of one of the most sweeping results in mathematics in recent years. It’s a proof by Tim Austin, a mathematician at the University of California, Los Angeles. Instead of flowers, Austin’s work has to do with some of the most-studied objects in mathematics: the mathematical descriptions of change.
These descriptions, known as dynamical systems, apply to everything from the motion of the planets to fluctuations of the stock market. Wherever dynamical systems occur, mathematicians want to understand basic facts about them. And one of the most basic facts of all is whether dynamical systems, no matter how complex, can be broken up into random and deterministic elements.
This question is the subject of the “weak Pinsker conjecture,” which was first posed in the 1970s. Austin’s proof of the conjecture provides an elegantly intuitive lens through which to think about all manner of bewildering phenomena. He showed that at their heart, each of these dynamical systems is its own blend of chance and determinism.
Fate and Chance
A dynamical system starts with some input, like the position of a pendulum right now, applies some rules, like Newton’s laws of motion, and produces some output, like the pendulum’s position a second later. Importantly, dynamical systems allow you to repeat this process: You can take the pendulum’s new position, apply the same rules, and get its position another second later.
Dynamical systems also arise in purely mathematical form. You could choose a starting number, apply a rule that says “multiply your number by 2,” and output a new number. This system also allows you to feed the resulting number back into the rule to produce more values.
Certain types of dynamical systems have the property that they can be expressed as a combination of two simpler dynamical systems. The two systems operate independently of one another but can be merged to form the more complex system. To take an example, imagine a dynamical system that moves a point around on the surface of a cylinder: You input one point, apply the rules, and get out another point.
This system can be decomposed into two simpler systems. The first is a dynamical system that moves a point around on a circle. The second is a system that moves a point up and down along a vertical line. By combining the two — the movement around the circle with the movement up and down the line — you get the more complicated movement of a point on a cylinder.
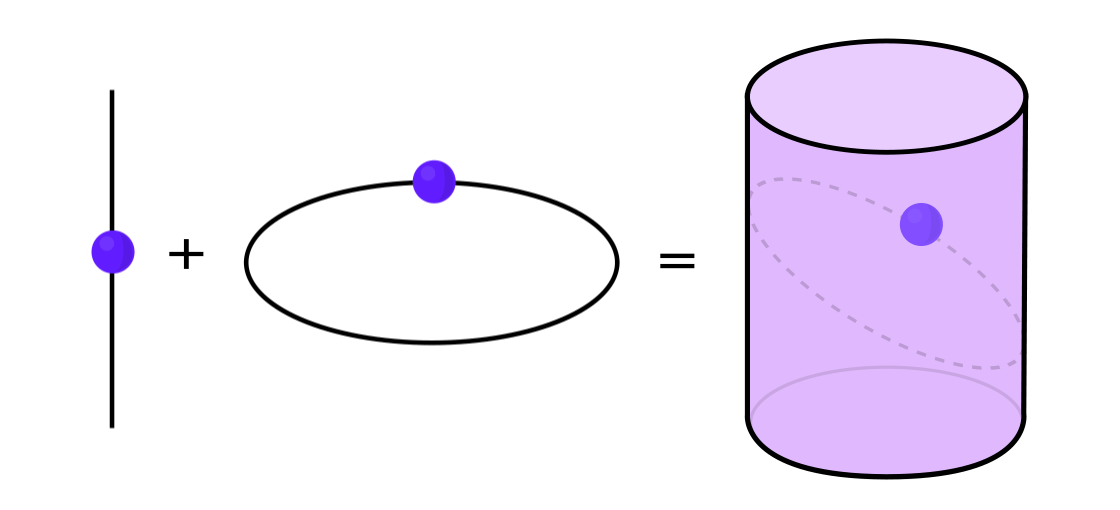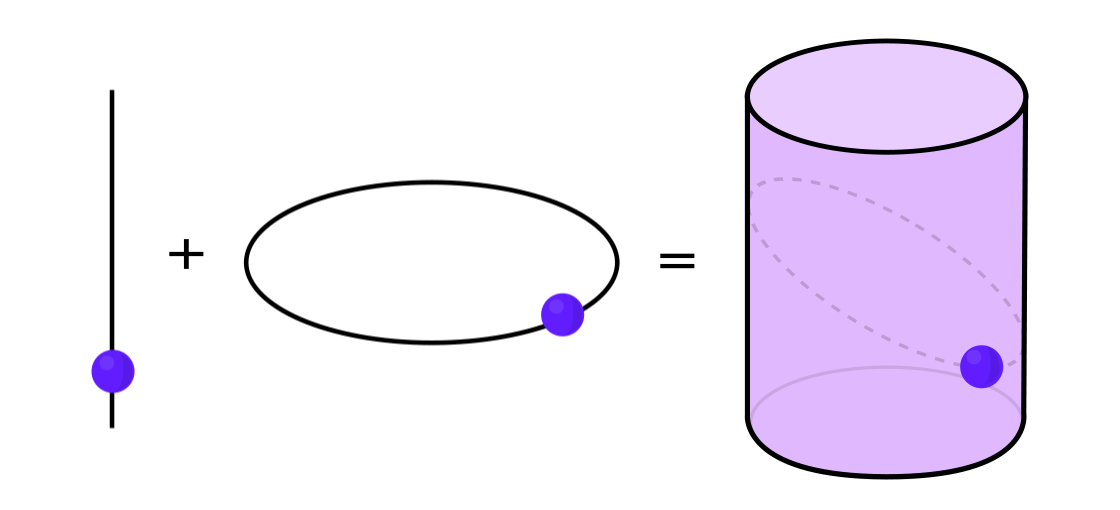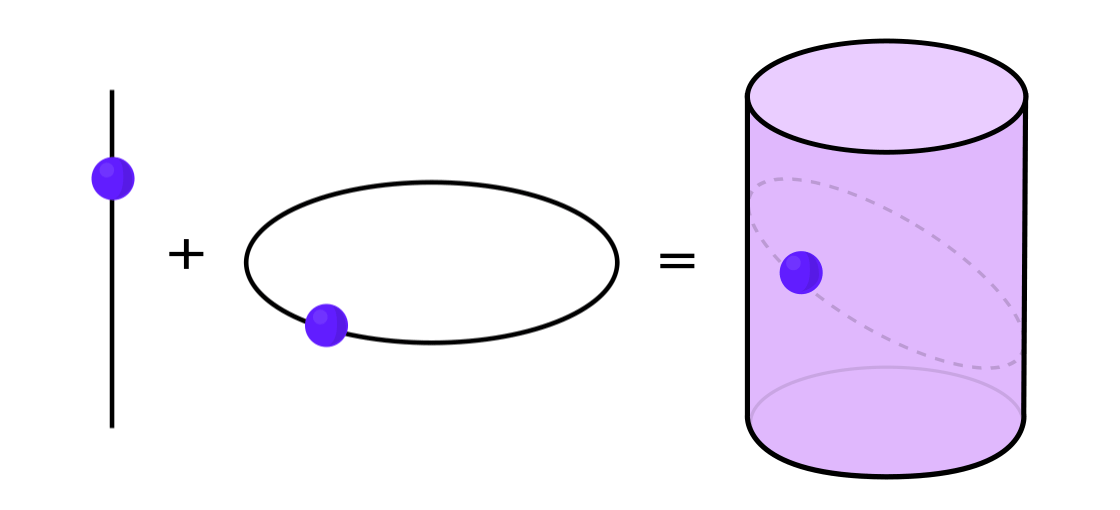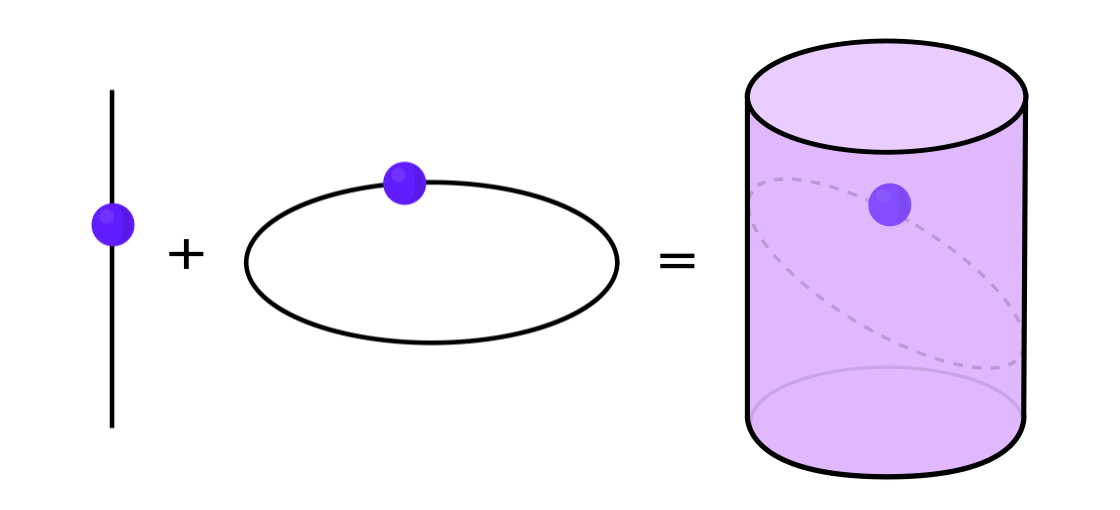
Credit: Lucy Reading-Ikkanda / Quanta Magazine.
“Rather than study the whole dynamical system, you want to break it into parts, the smallest parts that make sense to study,” said Kathryn Lindsey, a mathematician at Boston College.
There are two natural candidates for what these building blocks might be. The first are dynamical systems that are completely deterministic, like our example of the pendulum. If you know the position of the pendulum at one moment in time, you can predict its position indefinitely far into the future.
The second type of dynamical system is one that is completely random. For example, imagine a dynamical system with the following rule: Flip a coin. If it lands heads, walk to the left; if tails, walk to the right. The resulting path would be completely random, meaning that even if you know everything about the path up to a certain point, that information will do nothing to help you predict the next step.
While some dynamical systems are purely random, and others are completely deterministic, most fall somewhere in between — they’re blends of both. For example, imagine a twist on our random walk. This time, you’re on a flower-lined path where the colors of the flowers are themselves random. Our rule is the same: Coin flip comes up heads, move to the left; tails, move right. What is the sequence of colors of flowers that you visit?
At first you might think that it’s random. After all, the colors themselves have been assigned at random, and your motion is random. But once you have visited one color of flower, the odds are higher that you’ll visit that same flower again in the future, just by virtue of being close to it. The sequence of colors will not itself be purely random.
“If you’re at red right now, then that amplifies the chance you’ll see red two steps from now, because it could happen that you’ll go left and then right and end up back at the same place,” said Austin.
This “random walk in random scenery” system generates an output — a sequence of colors — that is partly random and partly not. In 1960 the mathematician Mark Pinsker conjectured that a certain large class of dynamical systems* have this feature: They’re each a mix of a random dynamical system mixed with a deterministic one.
“If the [original Pinsker conjecture] had been true, it would have been an amazing description of the world,” said Assaf Naor, a mathematician at Princeton University. Yet Pinsker was wrong. In 1973 Donald Ornstein proved Pinsker’s conjecture false. “It was an overly ambitious formulation,” said Bryna Kra, a mathematician at Northwestern University.
It often happens in math that after a sweeping conjecture is proven false, mathematicians attempt a more modest version of the statement. In 1977 mathematician Jean-Paul Thouvenot proposed the weak Pinsker conjecture. He softened the original formulation, conjecturing that the dynamical systems Pinsker had in mind are the product of a completely random system combined with a system that is almost completely deterministic.
The introduction of the qualifier “almost” distinguished Thouvenot’s conjecture from Pinsker’s. By it, he meant that the simple deterministic system needed to have at least a trace of randomness in it. That trace could be vanishingly small, but it needed to be there. And as long as it was, Thouvenot asserted, Pinsker’s vision would hold.
“It was close to the initial conjecture, and Thouvenot showed if it were true, it had a whole list of beautiful applications,” said Naor.
In the following decades, mathematicians made little progress on a proof of the weak Pinsker conjecture. The lack of traction started to make Thouvenot think that even his scaled-down formulation was going to turn out to be wrong. “At one point I thought it would go the opposite, it would not be universal,” he said.
Then Tim Austin came along.
A Stepwise Solution
Proving the weak Pinsker conjecture required finding a precise way to run a dynamical system through a kind of sieve — something that would separate its random and almost-deterministic elements. Previous work on the problem had established that the small random elements were the hardest to isolate.
“The small [random] factors are much harder to capture, and this is the heart of the proof, to find a way to capture the small [random] structure,” said Thouvenot.
Austin managed to understand the small, random elements in a dynamical system through a shift in perspective. Dynamical systems operate on continuous space, like a point moving over the surface of a cylinder or a pendulum swinging through space. Within these spaces, points move in continuous arcs according to the rules of the dynamical systems that govern them. These dynamical systems also continue for infinitely many steps — you can let them run forever.
But in his proof, Austin left smooth, continuous space behind and forgot about dynamical systems running forever. Instead he started to analyze what happens when you let them run for a discrete amount of time, like 1 million steps. In this, he was executing a method envisioned by Thouvenot.
“Thouvenot’s big contribution was that he figured out that if you can do the right kind of math with long finite strings” you can prove properties of the dynamical system, said Austin. “My contribution was to come in and prove the thing you need about the long finite strings.”
Austin thought about a dynamical system as outputting a sequence of 1s and 0s. If the dynamical system is the flip of a coin, it’s easy to see how to do this: Call heads 1 and tails 0. But any dynamical system can be used to generate a binary sequence, just by splitting the space in which it operates into two (not necessarily equal) parts.
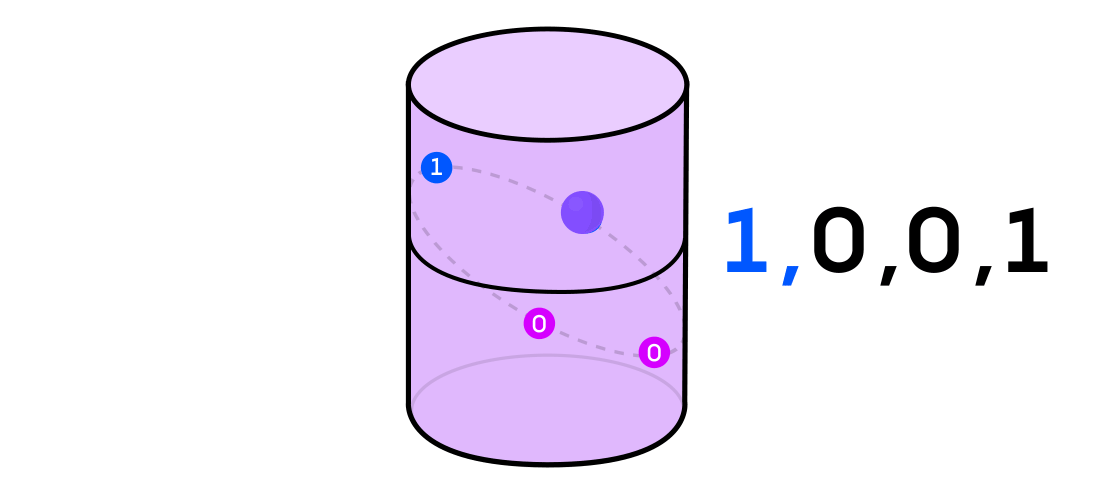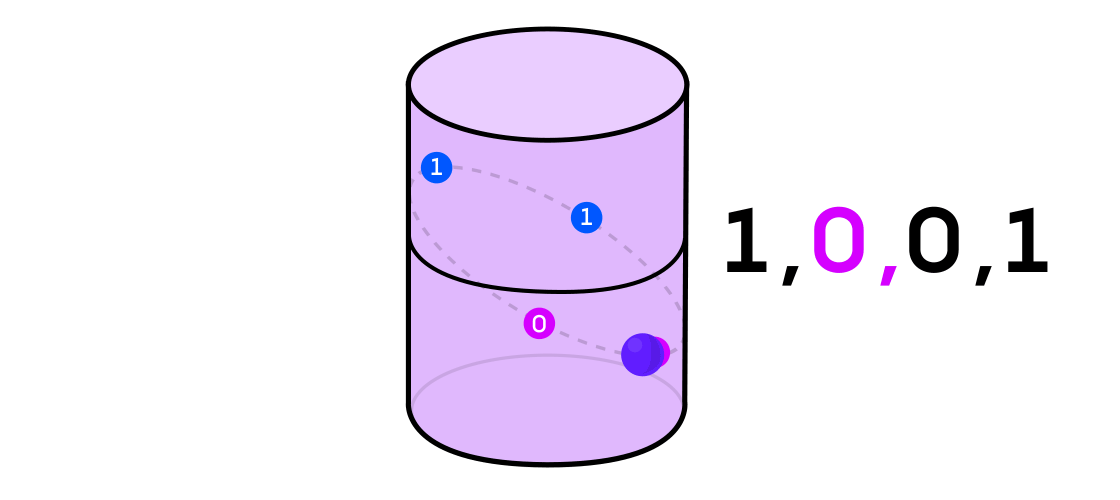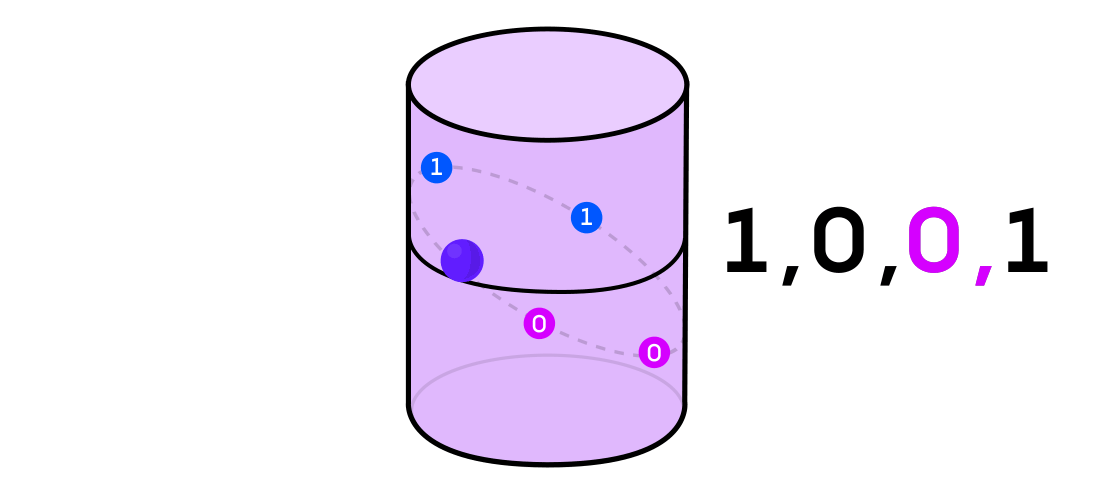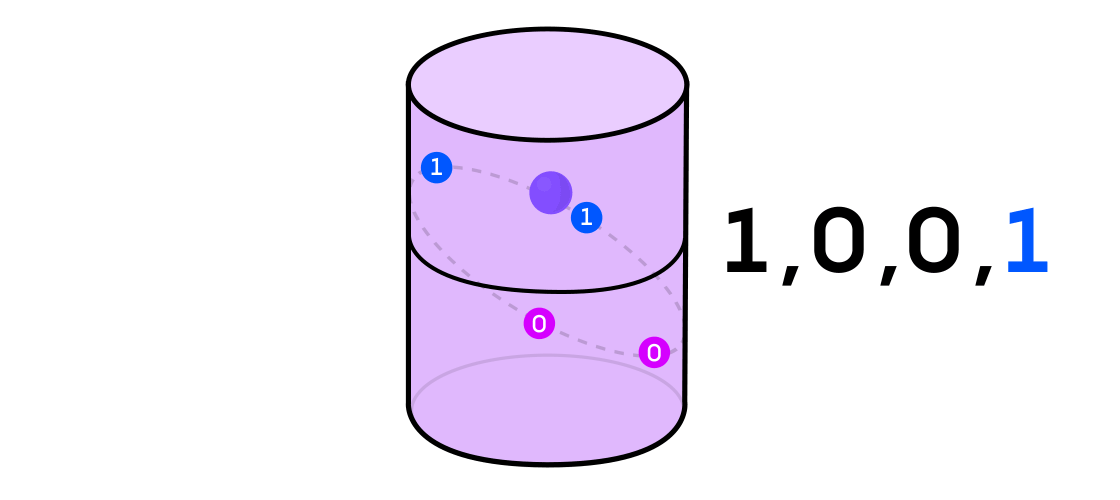
Credit: Lucy Reading-Ikkanda / Quanta Magazine.
With the example of a dynamical system on the cylinder, for instance, if your point lands in one part of the cylinder, you call the output of the system 1, and if it lands in the other part of the cylinder, you call the output 0.
Austin analyzed these binary sequences using a tool from information theory called “Hamming cubes.” Imagine a cube made by vertices connected by edges. Each vertex gets assigned three binary digits — 001 or 101, say. Every time you move from one vertex to another, one of those three digits will flip.
Hamming cubes can be far more complex than our simple example — involving far more edges and vertices in more than three dimensions — but they all have the property that the distance between any two vertices — that is, the number of edges that you need to traverse to get from one vertex to another — is equal to the number of places the strings of information on those two vertices differ. So 000 is one edge away from 001, two edges away from 011 and three from 111.

Credit: Lucy Reading-Ikkanda / Quanta Magazine.
In order to isolate the random and deterministic elements that make up a more complicated dynamical system, Austin thought about how frequently a dynamical system produces a given sequences of 1s and 0s as represented on the Hamming cube. He proved that the sequences are distributed on the Hamming cube in a certain way. They cluster into a small number of subregions on the cube — this clustering reflects the determinism in the system — but are distributed among the sequences within those clusters in a randomlike way, which reflects the system’s randomness.
The roundabout method turned out to be a necessary path for solving a problem that had defied direct approaches.
“I was surprised not so much that [weak Pinsker] is true or false, but that one could prove it, because it seemed like a very subtle problem,” said Lewis Bowen, a mathematician at the University of Texas, Austin. “Before the proof we were largely ignorant about whether something like this could be done.”
Austin’s result imposes a basic structure on a wide range of dynamical systems. For mathematicians, who often find themselves swimming among objects that feel related even if they can’t say exactly how, the proof reveals a strict geography. They now have a guide to these dynamical systems, though exactly what discoveries the guide will yield remains open.
“Mathematicians are always interested in what the building blocks of something are,” said Lindsey. “[Austin’s proof] is a really nice result that probably will have lots of applications in pure math, but I myself don’t know what they will be.”
Kevin Hartnett is a senior writer at Quanta Magazine covering mathematics and computer science.
* Pinsker’s conjecture applies to a class of dynamical systems that all share an essential property. With these systems, points neither spread out nor contract as the system evolves. More specifically, if you were to draw a loop around a set of points in your space (where your space could be something like the surface of a cylinder), run the dynamical system forward for a long time, and then draw a loop around the resulting set of points, you’d find that the area encompassed within the loop is the same at the beginning and the end. These systems are called “measure preserving” and are studied in a subfield of dynamical systems called ergodic theory.