For engineers, the question of whether to store information in analog or discrete form is easy to answer. Discrete data storage has clear advantages, not least of which is that it is much more robust against degradation.
Engineers have exploited this property. Provided noise is below some threshold level, digital music can be copied endlessly. By contrast, music stored in analog form, such as on cassette or vinyl LP, can be copied only a few times before noise degrades the recording beyond recognition.
The process of evolution has also exploited this advantage. DNA stores information in discrete form as a sequence of nucleotides and this allows the blueprint for life to be transmitted from one generation to the next with high fidelity.
So it’s easy to imagine that the question of how the brain stores information is easy to answer. Not so. Neuroscientists have long pondered this issue, and many believe that it probably uses some form of analog data storage. But the evidence in favor of discrete or analog data storage has never been decisive.
That's changed, at least in part, thanks to the work of James Tee and Desmond Taylor at the University of Canterbury in New Zealand. These guys have measured the way people make certain types of decisions and say that their statistical analysis of the results strongly suggests that the brain must store information in discrete form. Their conclusion has significant implications for neuroscientists and other researchers building devices to connect to the brain.
First, some background. One reason that neuroscientists are undecided on this issue is because neural signals are obviously analog in character. They generate analog electrical pulses in which the voltage potential varies between -40mV and -70mV at the cell membrane. So at first glance it’s easy to imagine that the data they carry is analog too.
That isn’t necessarily true. Electromagnetic signals are always analog at some level since it takes time for any circuit to switch from one state to another. However, the information encoded in these signals can be treated as discrete by ignoring these transitions.
So information transmitted along neurons could also be discrete. Indeed, there are good theoretical reasons to think it must be.
Back in 1948, the mathematician and engineer Claude Shannon published A Mathematical Theory of Communication, in which he showed how information stored in discrete form could be copied with arbitrarily small error, provided noise was below some threshold level.
By contrast, there is no equivalent theory for analog information, and attempts to approximate it by increasing the quantization of an analog signal into ever smaller parts suggest that it is nowhere near as robust. Indeed, Tee and Taylor say their theoretical analysis suggests that the brain cannot work like this. “It is impossible to communicate reliably between neurons under repeated transmissions using continuous representation,” they say.
But the experimental evidence that the brain stores data discretely has been lacking. But Tee and Taylor go on to say that if the brain stores information in discrete form, it should process it in a different way than analog information. And that should lead to a measurable difference in human behavior in certain decision-making processes.
In particular, Tee and Taylor focus on problems in which people have to make decisions based on their assessment of probabilities. If the brain is able to assess probabilities in a continuous way, this should lead to a range of human behavior that varies smoothly as the probabilities change.
However, if the human brain works on a discrete basis, it must treat some probabilities in the same way. For example, a person might judge probabilities as being low, medium, or high. In other words, the probabilities must be rounded into specific categories—probabilities of 0.23 and 0.27 might be treated as low, 0.45 and 0.55 as medium, and 0.85 and 0.95 as high, for example.
In that case the range of human behavior would follow a step-like structure that reflects the jump from low to medium to high risk.
So Tee and Taylor studied human decision-making as probabilities change. They did this by testing the way over 80 people judged and added probabilities associated with roulette wheels in more than 2,000 experimental trials.
The experiments employed a similar approach. For example, participants were shown a roulette wheel with a certain sector mapped out and asked to judge the probability of the ball landing in that sector. Then they were shown two wheels with different sectors mapped out. They had to judge the probability of the ball landing in both sectors. Finally, they were asked to judge whether the probability was higher in the case of the single roulette wheel or the double roulette wheel example.
The researchers then varied the size of sectors in the experiments to span a wide range of probabilities, in total carrying out 2,000 trials. Participants performed the tests in random order on a computer touch screen and were paid a token amount for their participation (although they also had the chance to win a bonus based on their performance).
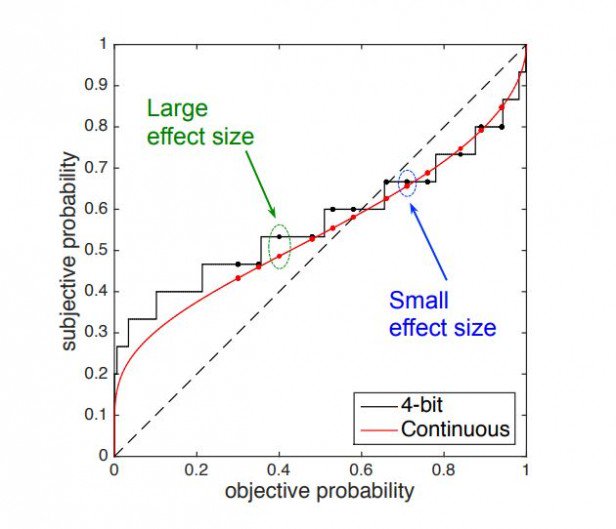
The results make for interesting reading. Tee and Taylor say that far from matching the smooth distribution of behavior expected if the brain stores information in analog form, the results are more easily interpreted using a discrete model of information storage.
An important factor is the extent to which the brain quantizes the probabilities. For example, does it divide them into three or four or more categories? And how does this quantization change with the task at hand? In that respect, Tee and Taylor say that a 4-bit quantization best fits the data.
“Overall, the results corroborate each other, supporting our discrete hypothesis of information representation in the brain,” conclude Tee and Taylor.
That’s an interesting result that has important consequences for future research in this area. “Going forward, we firmly believe that the correct research question to explore is no longer that of continuous versus discrete, but rather how fine-grained the discreteness is (how many bits of precision),” say Tee and Taylor. “It is very plausible that different parts of the brain operate at different levels of discreteness based on different numbers of quantization levels.”
Indeed, engineers have found this in designing products for the real world. Images are usually encoded with a 24-bit quantization, whereas music is generally quantized using a 16-bit system. This reflects the maximum resolution of our visual and auditory senses.
The work has implications for other areas too. There is increasing interest in devices that link directly with the brain. Such machine-brain interfaces will obviously benefit from a better understanding of how the brain processes and stores information, a long-term goal for neuroscientists. So research like this will help pave the way toward that goal.
Ref: arxiv.org/abs/1805.01631: Is Information in the Brain Represented in Continuous or Discrete Form?
Copyright © 2018. All rights reserved MIT Technology Review;
www.technologyreview.com.